OHD/HL - Distributed Model: DMIP

NWS Hydrologic Research Lab (HRL)
Distributed Model Intercomparison Project
(DMIP)

Draft Science Plan

August 2000

TABLE OF CONTENTS
 

EXECUTIVE SUMMARY......................................................................................... 3

1.0  INTRODUCTION............................................................................................... 4

 1.1  Background......................................................................................................... 4
 1.2   Major Goals....................................................................................................... 6
 1.3  Science Questions................................................................................................ 7
 1.4       Operational Questions..................................................................................... 7
 

2.0  EXPERIMENTAL DESIGN................................................................................ 7
 3.1   Plan Development............................................................................................... 7
 3.2       Plan Elements................................................................................................. 7

3.0  REFERENCES................................................................................................... 10
 

APPENDICES

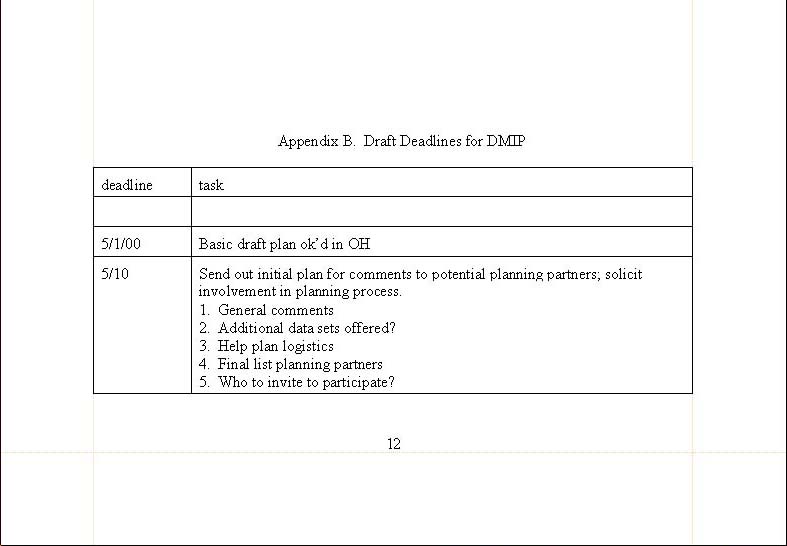
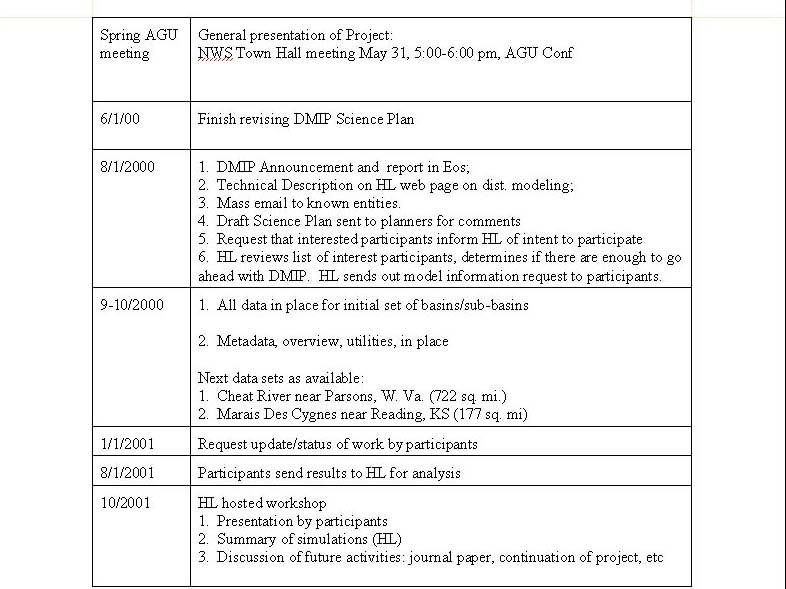
1.  Draft DMIP Milestones......................................................................................... 12
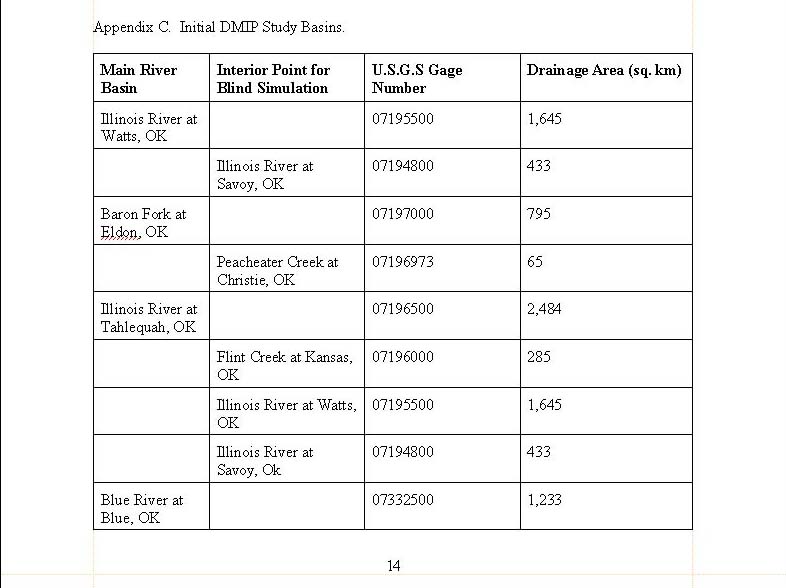
2.  Initial DMIP Study Basins...................................................................................... 14
 
 

EXECUTIVE SUMMARY

The Hydrologic Research Lab (HRL) of the National Weather Service (NWS) proposes the Distributed Model Intercomparison Project (DMIP).  The intent of DMIP is to invite the academic community and other researchers to help guide NWS distributed modeling research by participating in a comparison of distributed models applied to test data sets. HRL will provide data sets for several basins.   Participants will download the data sets and run their models in continuous simulation mode.  Model simulations will be compared to observed streamflow data as well as simulations generated from a lumped application of the Sacramento Soil Moisture Accounting (SAC-SMA) model.  Participants will be invited to meet in an HRL sponsored workshop to discuss results and future directions.  Results of DMIP will be used to guide future HRL distributed modeling research and application.
 

1.0   INTRODUCTION

1.1  Background

 Numerous studies have been conducted in the past two decades that point to the sensitivity of runoff hydrographs to spatial and temporal variations in precipitation. Many of these studies examined the effects of raingage sampling errors on the outflow hydrograph. In an early and oft-quoted work, Wilson et al., [1979] showed that the spatial distribution of rainfall had a marked influence on the runoff hydrograph from a small catchment. On the other hand, Beven and Hornberger [1982] stated that rainfall patterns have only a secondary effect on runoff hydrographs, while a correct assessment of the global volume of rainfall input in a variable pattern is more important in simulating streamflow hydrographs.  On a small watershed, Krajweski et al., [1991] found a higher sensitivity to the temporal resolution of precipitation than to the spatial resolution.   Ogden and Julien [1994] performed tests that identified when spatial and temporal variability of precipitation  was dominant.  Troutman, [1983],  Ogden and Julien [1994], and Shah et al.,[1996a,b] also investigated the effects of precipitation  variability on hydrologic simulations.
 It is interesting to note that the majority of these and other studies were based on synthetically generated precipitation and streamflow records.  Usually, comparisons were made against a ‘reference' or ‘truth' hydrograph generated by running the hydrologic model at the finest data resolution.  Synthetically generated data were often used due to the lack of appropriately long periods of observed data.  Moreover,  many of studies emphasizing the importance of the spatial variability of precipitation used models containing the Hortonian  runoff generation  mechanism. It is now recognized that runoff results from a complex variety of mechanisms and that in some basins, a significant portion of runoff hydrographs is derived from slower responding subsurface runoff [Wood et al., 1990].
 Obled et al., [1994] commented that numerical experiments in the literature were based on the use of models which may be only ‘a crude representation of reality'.  Furthermore, they argued that the actual processes at work in a basin may not be those predicted by  the model. Thus, the research in the literature may have shown the sensitivity of a particular model to the spatial variability of  precipitation,  not the sensitivity of the actual basin.  The  work of Obled et al, (1994) is significant in that they were perhaps the first to examine the effects of the spatial variation of rainfall using observed precipitation and streamflow data.  In addition, the model used in their studies focused on saturation excess runoff as the main runoff generation mechanism.  In simulations against observed data, they were unable to prove the value of distributed inputs as they had intended.  A semi-distributed representation of the basin did not lead to improved simulations compared to a lumped basin modeling scenario. The authors reasoned that the runoff mechanism may be responsible for the lack of improvement:

   "If, on the other hand, the dominant process involves either surface or subsurface contributing areas of the Dunne type, then most of the water infiltrates and local variations in input will be smoothed as the water is stored and delayed within the soil.....this type of mechanism may be much less sensitive to different rainfall patterns at the scale of small catchments"

  Winchell et al [1998] and Winchell et al.,[1997]  extend this theme by noting that there has been a bias towards the use of infiltration-excess runoff mechanisms as opposed to the saturation excess type.  Their work with both types of runoff generation mechanisms  found that saturation-excess and infiltration excess models respond differently to uncertainty in precipitation.  They suggest that generalizations concerning the effects of rainfall variability on runoff generation cannot be made.  Koren et al., [1999] came to a similar conclusion based on simulation results from several different rainfall-runoff partitioning mechanisms.
 Nonetheless, a large volume of  research continues to emerge that addresses the possibility of improving lumped  hydrologic simulations by using distributed and semi-distributed modeling approaches which account for the spatial variation of not only physiographic basin features but of precipitation as well.  Recently, the availability of high resolution precipitation estimates from different weather radar platforms has intensified this investigation. Most efforts have focused on event-based modeling and mixed and somewhat surprising results have been realized compared to the numerical results discussed above.
 Pessoa et al., [1993] found that adequately averaged gridded precipitation estimates from radar  were just as viable as fully distributed estimates for streamflow simulation using a distributed model.  Kouwen and Garland [1989] investigated the effects of radar data resolution and attempted to develop guidelines for the proper resolution of input rainfall data resolution.  They noted that spatially coarser rainfall data sometimes led to better hydrograph simulation due to the smoothing of errors present in finer resolution rainfall information.  In preliminary testing limited to a single extreme event, Kenner et al., [1996] reported that a 5 sub-basin approach produced better hydrograph agreement than a lumped representation of the basin.  Sub-basin rainfall hyetographs revealed spatially varied precipitation totals for the event. Refsgaard [1997] illustrated the concepts of parameterization, calibration, and validation of distributed parameter model.  Noting that hydrologists often assume that a distributed model calibrated to basin outlet information will adequately model interior processes, he realized poor simulations of discharge and piezometric head at 3 interior gaging stations.
 In contrast, Michaud and Sorroshian [1994] found that a complex distributed model calibrated at the basin outlet was able to generate simulations at 8 internal points that were at least as accurate as the outlet simulations. These results underscore one of the mains advantages of distributed parameter hydrologic modeling: the ability to predict hydrologic variables at interior points.  They also concluded that a simple distributed model proved to be just as accurate as a complex distributed model given that both were calibrated and noted that model complexity does not necessarily lead to improved simulation accuracy.
 It is a concern that few of the studies have shown a direct comparison of distributed model and lumped model results to observed streamflow data.  The emergence of high resolution data sets, GIS capabilities, and rapidly increasing computer power have pushed distributed hydrologic models to the forefront of research and development. While the utility of distributed models to predict interior hydrologic processes is well known, few studies have specifically addressed the improvement of distributed models over lumped models for predicting basin outflow hydrographs. As a consequence, the hypothesis that higher resolution data will lead to more accurate hydrograph simulations  remains largely untested.
 A few years ago, the Hydrologic Research Laboratory (HRL) of the NWS began a major research effort to address the question: ‘How can the NWS most effectively utilize the NEXRAD data to improve its river forecasts?'  In Phase I of this research, modeling tests have involved existing NWS hydrologic models applied in a lumped and semi-distributed format.  The model used in these efforts was the  Sacramento Soil Moisture Accounting Model (SAC-SMA).   In Phase 2, new models such as gridded distributed models will be examined and developed.
 In the Phase 1 semi-distributed simulations, several RFC scale basin were disaggregated into 5 to 8 sub-basins in an effort to capture the spatial variability of precipitation and soil/vegetation properties (Smith et al., 1999).  Simulations from lumped and semi-distributed approaches were compared to observed data for five basins (with drainage areas ranging from 820 to 4200 sq. km.) using results of continuous simulations over a period of 4-6 years. The analyses suggest that the spatial rainfall averages derived from NEXRAD data can improve flood prediction in mid/large basins as compared to gage-only averages.  While the semi-distributed approach shows potential for improved hydrograph simulation, parameterization problems and noisy data can eliminate benefits when applied to mid/large basins having significant damping effects (e. g., those caused by deep, well drained  soils).  A more noticeable benefit from the semi-distributed approach is achieved for basins with a fast response runoff (Smith et al, 2000)  However, optimal model parameters from the lumped approach may be far from the  optimal parameter set for the semi-distributed approach.
 It is clear that distributed modeling is in the future.  However, there is no clear pathway in the literature towards distributed models that will suit NWS forecasting needs.  To address this problem and the other issues mentioned above,  HRL is initiating the Distributed Model Intercomparison Project (DMIP).   The intention is to access broad scientific community experience to help guide NWS/HRL distributed modeling research and application.  Within DMIP, HRL will make available data sets for a number of basins.  Participants will download the data sets and run their models to generate simulations at specific locations.  HRL will generate statistics comparing the simulations to observed streamflow as well as to simulations from a calibrated lumped SAC-SMA model.  Participants will be invited to a workshop at  HRL to present their models and results.  The workshop will also provide opportunities to discuss further research and publication of results.
 

1.2 Major Goals of DMIP

A.   To develop methods to optimally utilize NEXRAD and other spatial sets data to improve RFC scale river simulations

B.    To help guide NWS HL future hydrologic distributed  modeling research, science, and application.
 

1.3   Science Issues

 Among the science issues that could be addressed by an intercomparison of distributed modeling approaches are:

 1.  What characteristics identify a basin as one likely to benefit from distributed  modeling (i.e., accounting for the spatial variability of precipitation and model parameters)?  Can these characteristics be identified?
 2. What is the tradeoff in computational element size required to capture the essential spatial variability of precipitation versus the size required to route runoff to stream channels?
 3.  What level of model complexity is required to realize improvement in basin outlet simulations?
 4.  What is the potential for distributed models set up for basin outlet simulations to generate hydrographs at interior locations for flash flood forecasting?
 5.  Which  approaches work well for handling sub-grid heterogeneity of hydrologic variables?

1.4   Operational Issues

 Issues that need to be addressed before a model can be implemented in NWSRFS for operational use are:

 1.  Computational requirements in an operational  environment
 2.  Run time modifications and updates in an operational forecasting setting.
 3.  Parameterization and calibration requirements.
 4.  Does ease of parameterization/calibration of a physically based distributed parameter model warrant its use, even when it might not provide improvements over simpler (but harder to calibrate) lumped conceptual models?
 

2.0 EXPERIMENTAL DESIGN

2.1 Plan Development: HL will work with specific outside agencies/institutions to help design the project.

2.2  Proposed Plan Elements

  A.   Model Simulations:
  Participants will generate hydrographs in two ways:
   A.  Simulations using uncalibrated versions of their model.
   B.  Simulations using models calibrated at basin outlet.
 

  1.  Participants will test their models on basins (200-2500 sq. km.)  to produce basin outlet hydrographs.
  2.  Where observed data are available, models will also produce a ‘blind' simulation at interior sub-basin points as a test of providing answers at ungaged sites.  Participants will not perform explicit calibration above these points.  See Appendix 3 for a listing of the proposed interior sites.
  3.  Models will produce simulations at HL specified interior ungaged points to assess variability of predictions amongst models.

  B   Models will be run in continuous retrospective simulation mode.  Calibration period will be from 1993 (or date of earliest sound data) to May, 1999.  Verification period June, 1999 to present .
 C.  Basins will be limited to those in used by HL distributed modeling research
 D.  Basic data sets will be provided by HL  on web or ftp site
 E.  Participants will model one or more basins to produce a deterministic simulation.
 F.  Participants will submit their simulations to HL in a standard format.  HL will produce a comprehensive analysis of all simulations compared to observed data and lumped SAC-SMA simulations.  This analysis will be presented at HL hosted workshop.
 G.   Standard: Simulations from participants' models will be compared to those generated from a calibrated lumped SAC-SMA model.
 H.  It is envisioned that a paper describing the results of the workshop will be submitted  to a  peer-review journal.  Participants will be coauthors.  It is hoped that a special issue of a journal would be dedicated to the results of DMIP.
 I. Evaluation Criteria: standard statistical measures for hydrograph comparison will be used.

2.3 Data Types  Provided by HL

 A.   DEM: resolution is 400 m. in Albers Equal Area Projection. Higher resolution data such as the 30 m. data from USGS could be made available.
 B   Basin Boundary LAT/LON pairs
 C.   LAT/LON location of interior computational points.
 D.   Hourly streamflow from USGS.
 E.   NEXRAD Stage III xmrg files and utilities for usage
 F. NRCS Soils (Derived by D. Miller from STATSGO)
 G. Energy forcing fields (possibly from NCEP regional re-analysis)
 H.     Vegetation
 I.   NDVI-5 Greenness Fraction Data
 J.     Other, as donated by participants

 Participants needing other data will be responsible for obtaining them.
 

2.4 Workshop at OH: we will ‘host' a workshop after a specified period of time where participants will present their results and discuss the following:
 A. Model Overview
 B. Model parameterization
 C Model calibration
 D.  Computational Time
 E.   Comparison Statistics: 1)  at parent basin outlet,  2) at interior points where observed streamflow data is available; 3)  HL designated points for variability assessment.  Comparison statistics will be generated using observed flow records and the calibrated lumped application of the SAC-SMA model.
 F.  Future modeling studies; publication of results; special issue of journal.
 

2.5 Funding: HL will  "host" this intercomparison, not "support" it, i.e., HRL will supply the organizational legwork but participants should look for some funds from their own or other organizations.
 

4.0  REFERENCES

Beven, K.J., and G.M. Hornberger,   Assessing the effect of spatial pattern of precipitation in modeling stream flow hydrographs, Water Resources Bulletin, 823-829, 1982.

Koren, V. I., B.D. Finnerty, J.C. Schaake, M.B. Smith, D.J. Seo, Q.Y. Duan, Scale dependencies of hydrology models to spatial variability of precipitation, Journal of Hydrology, 217, 285-302, 1999.

Krajewski, W.F., V. Lakshmi, K.P.  Georgakakos,  and S. C. Jain,  A monte -carlo study of rainfall sampling effect on a distributed catchment model, Water Resources Research, Vol. 27, No. 1, 119-128, 1991.

Michaud, J., and S. Sorooshian, Comparison of simple versus complex distributed runoff models on a midsized semiarid watershed, Water Resources Research, Vol. 30, No. 3. 593-605, March, 1994.

Obled, C.H., J. Wendling, and K. Beven, The sensitivity of hydrological models to spatial rainfall patterns: an evaluation using observed data, Journal of Hydrology, 159,305-333, 1994.

Ogden, F.L., and P.Y. Julien,  Runoff sensitivity to temporal and spatial rainfall variability at runoff plane and small basin scales, Water Resources Research, Vol. 29, No. 8, 2589-2597, 1993

Ogden, F.L, and P.Y. Julien, Runoff model sensitivity to radar rainfall resolution, Journal of Hydrology, 158, 1-18, 1994.

Pessoa, M.L., R.L, Bras,.  and E.R. Williams, Use of weather radar for flood forecasting in the sieve river basin: a sensitivity  analysis, Journal of Applied Meteorology, 32 (3), 462-475, 1993.

Refsgaard, J.C., Parameterisation, calibration, and validation of distributed hydrological models, Journal of Hydrology, (198), 69-97, 1997.

Shah, S.M.S., P.E. O'Connell,  and J.R.M Hosking,  Modeling the effects of spatial variability in rainfall on catchment response. 1.  Formulation and calibration of a stochastic rainfall field model, Journal Hydrology, 175, 66-88, 1996a.

Shah, S.M.S., P.E. O'Connell,, and J.R.M. Hosking,,  Modeling the effects of spatial variability in rainfall on catchment response. 2. Experiments with distributed and lumped models, Journal of Hydrology, 175, 89-111, 1996b.

Smith, M.B., V.I. Koren, Z. Zhang, D. Wang, S. Reed., 2000, ‘Semi-distributed vs Lumped Model Simulations: Comparisons Using Observed Data for RFC Scale Basins', EOS, Transactions of the American Geophysical Union, 2000 Spring Meeting, Vol., 81, No. 19. Abstract only.

Smith, M. B, V. Koren, D.  Johnson, B.D.  Finnerty, and D.J. Seo,  Distributed Modeling: Phase 1 Results, NOAA Technical Report NWS 44, 210 pp.,  National Weather Service  Hydrologic Research Lab, February 1999.
 

Troutman, B.M., Runoff Prediction Errors and Bias in Parameter Estimation induced by Spatial Variability of Precipitation, Water Resources Research, Vol 19. No. 3,  791-810, 1983.

Wilson, C.B., J.B. Valdes, and I. Rodriquez-Iturbe, On the Influence of the spatial distribution of rainfall on storm runoff, Water Resources Research, Vol 15(2), 321-328, 1979.

Winchell, M., H.V.  Gupta,  and S. Sorooshian, Effects of radar-estimated precipitation uncertainty on different runoff generation mechanisms, Rep. HWR No. 97-080, 285 pp., Department of Hydrology and Water Resources, University of Arizona, 1997.

Winchell, M., H.V. Gupta, and S. Sorroshian, ‘On the simulation of infiltration- and saturation-excess runoff using radar-based rainfall estimates: Effects of algorithm uncertainty and pixel aggregation',  Water Resources Research, Vol 34, No. 10, 2655-2670, 1998.

Wood, E.F., M. Sivapalan, and K. Beven, Similarity and scale in catchment storm response, Review of Geophysics, 28(1),  1-18, 1990.