Mark A. Rose
WFO Nashville, TN
1. Introduction
In 1997, Massie and Rose investigated the operational usefulness of using 1000-850 mb thicknesses in forecasting maximum temperatures at Nashville, Tennessee (OHX). Since the publication of this study in Weather and Forecasting (1997), the Massie/Rose method has been used with much operational success. It was therefore decided to undertake a second study where the feasibility of using 1000-925 mb thicknesses to forecast minimum temperatures would be investigated.
This paper will outline the methodology used in gathering and processing the data. Results will also be presented, including operational usefulness. Conclusions will be discussed, primarily focusing on the derived regression equation applied to model forecast thicknesses to obtain minimum temperatures, and correction factors applied to the derived minimum temperatures.
2. Methodology
Thickness values of the 1000-925 mb layer were collected for 1999 using OHX sounding data collected at 1200 UTC. These thicknesses were then correlated with observed minimum temperatures derived from the additive data of the six-hourly OHX surface observations taken at 0600 and 1200 UTC each day. A total of 352 cases were collected. (Thirteen 1200 UTC soundings were unsuccessful at OHX during 1999.) Data for each case were entered into a Lotus 1-2-3 spreadsheet so that a day-by-day account of observed 1000-925 mb thicknesses and observed minimum temperatures could be created and manipulated.
3. Results
In order to test for a relationship between 1000-925 mb observed thicknesses and corresponding observed minimum temperatures, a correlation coefficient (r2) was calculated encompassing all 352 cases. The r2 was found to be 0.892, which suggests a strong linear relationship between the fields (Figure 1). Correlation coefficient is represented by the following equation (Mendenhall 1991),
| r2 = Sxy2/SxxSyy | (1), |
where Sxx is the sum of the squares of deviations about the "x" predictor, Syy is the sum of the squares of deviations about the "y" predictor, and Sxy is the sum of the deviations about the "x" and the "y" predictors.
Additional statistical calculations were done to further test the feasibility of using the data operationally. A regression equation was calculated using thicknesses and minimum temperatures as predictors. This regression equation is,
| Tmin = 0.667 * Tk1000-925 mb - 387 | (2), |
where Tmin is the minimum temperature estimated from the thickness value, and Tk1000-925 mb is the 1000-925 mb thickness value.
The regression equation was then applied to the data so that Tmin could be derived for each day. These values were then compared to the corresponding observed miminum temperatures. Standard error of estimation (E) is represented by the following equation,
| E = Tmin - Tobs | (3), |
where Tobs is the observed minimum temperature. The average standard error of estimation (Emean) for all 352 cases was 5.1oF. The standard deviation for all values of E was also 5.1oF. Standard deviation (s) is represented by the following equation (Mendenhall 1991),
| s = (Σ(xi - xmean)/(n - 1))1/2 | (4), |
where xi is the standard error of estimation, and xmean is the average standard error of estimation.
Since the cool seasons in Nashville generally have the most variable nighttime cloud conditions, it was decided to segregate the data by season and test a linear regression for each season. For this study, the months January, February, and December represent winter, March, April, and May represent spring, June, July, and August represent summer, and September, October, and November represent autumn. This breakdown resulted in lower r2 values (Figures 2, 3, 4, and 5). Again, the r2 for all cases was 0.892. The breakdown resulted in the following seasonal r2 values: winter (0.806), spring (0.827), summer (0.605), autumn (0.720). Thus it was decided to continue using equation 2.
(One reason for the lower seasonal r2 values relative to the complete data set is that the complete data set represents a much broader x-intercept than each seasonal subset, thereby accounting for a larger r2.)
To see if changes in surface albedo might contribute to some of the seasonal fluctuations in temperature, especially relative to nights exhibiting good radiational cooling, it was decided to research existing studies on seasonal effects of albedo on temperature. The only such studies uncovered dealt with the effects of snowcover on temperature (Carleton 2000). Several references on this topic exist. However, the underlying conclusion is that sustained snowcover, lasting a couple of weeks, will tend to depress surface temperatures (and, by implication, tropospheric thickness). Since Nashville does not experience prolonged episodes of snow cover, this effect is believed to be negligible or non-existent. Information on possible variations in surface albedo caused by seasonal changes in vegetative cover was unavailable.
4. Correction Factors
In an effort to further reduce the standard deviation, it was decided to derive a set of "correction factors" to be based on the predominant meteorological state for each case. Predominant means that the meteorological state was observed for more than six hours in the twelve hour period ending at 1200 UTC each day. Six such meteorological states were used:
1) radiational cooling, consisting of clear or scattered clouds and prevailing wind speed of 4 knots or less;
2) "supressed" radiational cooling, where broken or overcast cirrus or prevailing wind speeds 5 knots or greater (but less than 10 knots) would have tempered the effects of radiational cooling;
3) prevailing wind speeds 10 knots or greater, but in the absence of broken or overcast low clouds or precipitation;
4) broken or overcast mid clouds, i.e., altocumulus and/or altostratus (above 6,500 feet AGL to approximately 17,000 feet);
5) broken or overcast low clouds (up to 6500 feet AGL);
6) precipitation.
The following list contains a month-by-month listing of observed meteorological states (numbered 1-6, as described above).
| Month | Cases | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| January | 30 | 4 | 4 | 6 | 0 | 11 | 5 |
| February | 23 | 1 | 11 | 0 | 3 | 6 | 2 |
| March | 30 | 4 | 11 | 0 | 3 | 8 | 4 |
| April | 29 | 3 | 10 | 4 | 9 | 2 | 1 |
| May | 31 | 10 | 9 | 0 | 9 | 2 | 1 |
| June | 30 | 4 | 16 | 1 | 6 | 2 | 1 |
| July | 31 | 13 | 11 | 0 | 5 | 2 | 0 |
| August | 31 | 16 | 10 | 0 | 4 | 1 | 0 |
| September | 30 | 13 | 10 | 0 | 6 | 1 | 0 |
| October | 30 | 14 | 11 | 0 | 1 | 3 | 1 |
| November | 27 | 8 | 14 | 0 | 0 | 2 | 3 |
| December | 30 | 5 | 12 | 1 | 4 | 6 | 2 |
| Total | 352 | 95 | 129 | 12 | 50 | 46 | 20 |
Emean was calculated for each of the meteorological data subsets (cases 1-6).
Emean for meteorological state 1 (95 cases) was +3.5oF, which means the regression equations overestimated the minimum temperature by an average of 3.5oF when conditions promoting radiational cooling predominated.
For meteorological state 2 (129 cases), Emean was +0.2oF, which suggests that broken or overcast cirrus or prevailing winds of 5-9 knots tend to temper the effects of radiational cooling (here, by an average of 2.8oF).
Emean for meteorological state 3 (12 cases) was -3.8oF, which suggests that prevailing wind speeds of 10 knots or greater resulted in an underestimation of minimum temperatures by the regression equations. This is likely the result of increased mixing of boundary layer air. (It is understood that the limited number of cases here may diminish the reliability of Emean for meteorological state 3.)
For meteorological state 4 (50 cases), Emean was -3.2oF. This suggests that broken or overcast mid clouds also resulted in an underestimation of minimum temperatures by tempering or preventing radiational cooling from occurring.
Emean for meteorological state 5 (46 cases) was -4.7oF, which suggests that broken or overcast low clouds may play an even more important role in minimum temperature forecasting than mid clouds.
For meteorological state 6 (20 cases), Emean was -4.0oF. The effect of precipitation, on average, causes less deviation from Tmin than what was observed in case 5. This suggests that these departures may be independent of the type of clouds accompanying the precipitation. Minimum temperatures occurring during this meteorological state were, on average, 0.7 degrees cooler than those occurring during meteorological state 5. The effects of evaporative cooling may be at least partially responsible for this difference, although significance testing was not performed in order to prove such a conclusion. (It is again understood that the limited number of cases here may diminish the reliability of Emean for meteorological state 6.)
Most importantly, when the correction factors were inserted into equation 2, "s" improved from 5.1oF to 4.2oF.
5. Conclusions
A strong linear relationship between observed 1200 UTC 1000-925 mb thickness and corresponding observed minimum temperature does exist. This relationship can be expressed statistically, and the results may be applied successfully to an operational forecast.
Correction factors can be applied for specific forecast meteorological states to further refine a minimum temperature forecast based on the 1000-925 mb thickness.
When applying these techniques to model data, one must compare model initialized 1000-925 mb thickness to the observed thickness gained from sounding data. Model errors and/or biases introduced into the initialization will likely propagate throughout the model run, so forecasts based on thickness trends (i.e., 24-hour changes) may be more applicable.
Acknowkedgements
The author thanks Darrell Massie, Lead Forecaster, and Henry Steigerwaldt, Science and Operations Officer, WFO Nashville, for their suggestions, Mike Girodo, Lead Forecaster, WFO Nashville, for his review, and Dr. Scott Kirsch, Associate Professor, Department of Geography, University of Memphis, for his assistance in locating references. A very special thanks goes to Dr. Andrew Carleton, Professor, College of Earth and Mineral Sciences, Penn State University, for his assistance with albedo.
References
Carleton, A. Personal Communication. 10 March 2000.
Massie, D. and M. Rose, 1997: Predicting daily maximum temperatures using linear regression and Eta geopotential thickness forecasts. Wea. Forecasting, 12, 799-807.
Mendenhall, W. and R. Beaver, 1991: Introduction to Probability and Statistics. PWS-Kent Publishing Company, Boston, Massachusetts, 716 pp.
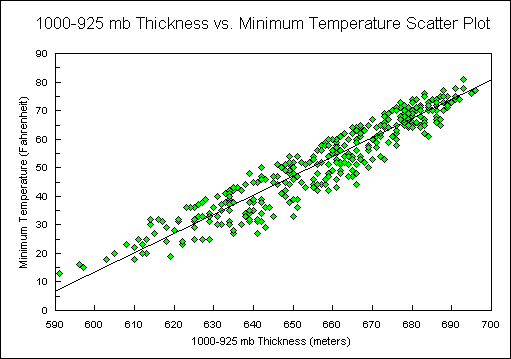
Figure 1.
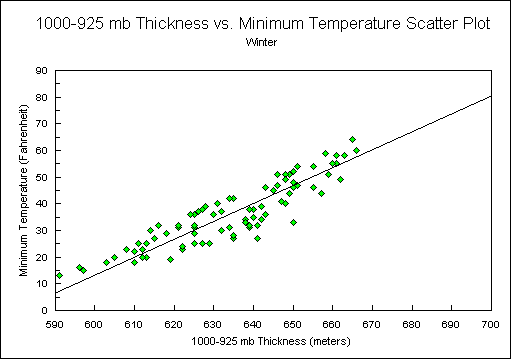
Figure 2.
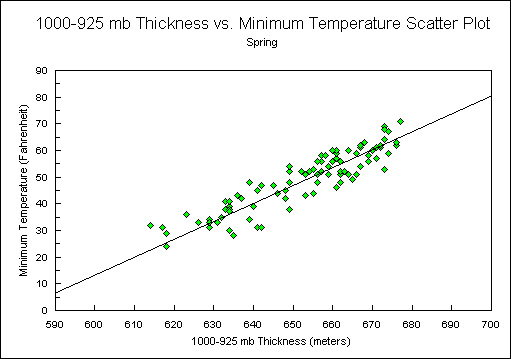
Figure 3.
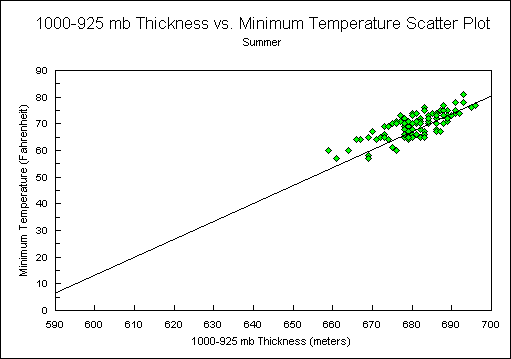
Figure 4.
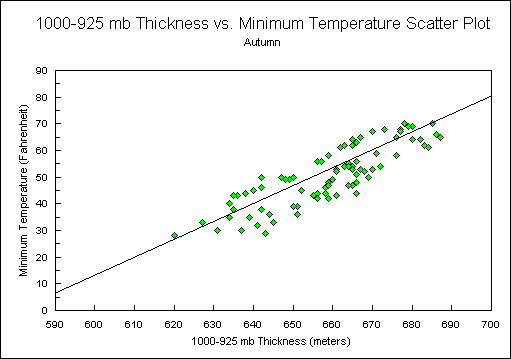
Figure 5.